Summary
- One-month forward Swedish Government Bond rates peaked at 2.50% this week, compared to 2.58% the previous week.
- The 2-year/10-year Swedish Government Bond spread closed the week at 0.271%, compared to 0.32% one week prior.
- The most likely one percent range for the 3-month yield in ten years is unchanged from last week: 0% to 1%. The most likely one percent range for the 5-year yield four and one-half years forward is 1% to 2%, which is also unchanged from last week.
- The simulation with U.S. Treasuries shows a Krona/U.S. Dollar exchange rate at a median value of 0.0876 and a standard deviation of 0.0049 one year forward.
- The same simulation is used to price short and long-dated foreign exchange options on the Krona versus the U.S. dollar at a strike price of 0.0910.
Author’s Note
This simulation has been done jointly with a U.S. Treasury yield simulation in a way that reflects the correlation among the 8 Swedish factors and the12 U.S. factors driving yields. For more on the companion U.S. Treasury simulation, please contact the author. Both the Government Bond and the U.S. Treasury yield simulations impact foreign exchange rates, resulting in the following distribution of the Krona/U.S. dollar exchange rate one year forward. Note this graph shows the Krona cost of 1 U.S. dollar:

Pricing for short- and long-dated European and American options to buy Kronas versus U.S. dollars at a strike price of 0.0910 for quarterly maturities out to 10 years is shown below. Note that the data for American options is the lower bound on the fair-value price.

This Week’s Simulation of Government Bond Yields
As explained in Prof. Robert Jarrow’s book cited below, forward rates contain a risk premium above and beyond the market’s expectations for the 3-month forward rate. We document the size of that risk premium in the graph below, which shows the zero-coupon yield curve implied by current Swedish Government Bond prices compared with the annualized compounded yield on 3-month bills that market participants would expect based on the daily movement of government bond yields in 14 countries since 1962. The risk premium, the reward for a long-term investment, is positive and remains so over the full maturity range to 10 years. The graph also shows a steady downward shift in current zero-coupon yields in the first three years, as explained below, followed by a more gradual decrease.
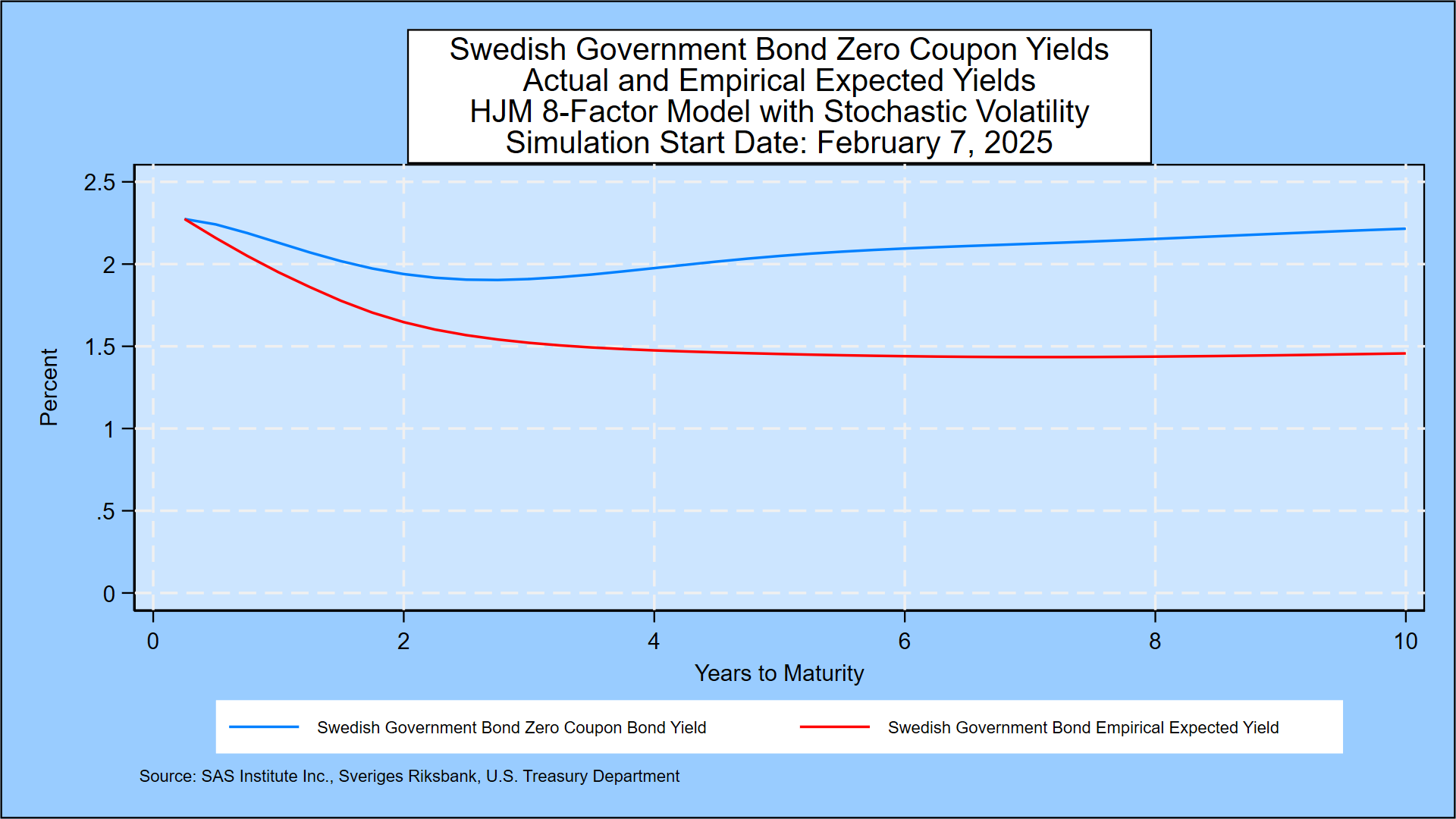
For more on this topic, see the analysis of government bond yields in 14 countries through December 31, 2024 given in the appendix.
Inverted Yields, Negative Rates, and Sweden Government Bond Probabilities 10 Years Forward
In this week’s Swedish market simulation, the focus is on the probability distribution of Swedish Government Bond yields over the next decade.
We start from the closing Swedish Government Bond yield curve published daily by the Sveriges Riksbank and other information sources. Using a maximum smoothness forward rate approach, Friday’s implied forward rate curve shows 1-month rates at an initial level of 2.29%, compared to 2.31% last week. As maturities lengthen, rates peak at 2.50%, compared to 2.58% last week. At the end of the 10-year horizon, the 1-month forward rate is 2.50%, versus 2.58% last week.

Using the methodology outlined in the appendix, we simulate 100,000 future paths for the Swedish Government Bond yield curve out to ten years.
Calculating the Default Risk from Interest Rate Maturity Mismatches
In light of the interest-rate-risk-driven failure of Silicon Valley Bank in the United States on March 10, 2023, we have added a table that applies equally well to banks, institutional investor, and individual investor mismatches from buying long-term Sweden Government Bonds with borrowed short-term funds. We assume that the sole asset is a 7. We analyze default risk for four different initial market values of equity to market value of asset ratios: 5%, 10%, 15%, and 20%. For the banking example, we assume that the only class of liabilities is deposits that can be withdrawn at par at any time. In the institutional and retail investor case, we assume that the liability is essentially a borrowing on margin/repurchase agreement with the possibility of margin calls. For all investors, the amount of liabilities (95, 90, 85 or 80) represents a “strike price” on a put option held by the liability holders. Failure occurs via a margin call, bank run, or regulatory takeover (in the banking case) when the value of assets falls below the value of liabilities.
The chart below shows the cumulative 7-year probabilities of failure for each of the 4 possible capital ratios when the asset’s maturity is 10 years. For the 5 percent case, that default probability is 29.01%.

This default probability analysis is updated weekly based on the Swedish Government Bond yield simulation described in the next section. The calculation process is the same for any portfolio of assets with credit risk included.
Swedish Government Bond Yield Probabilities 10 Years Forward
In this section, the focus turns to the decade ahead. This week’s simulation shows that the most likely range for the 3-month bill yield in the Government Bond market in ten years is from 0% to 1%, unchanged from last week. There is a 30.37% probability that the 3-month yield falls in this range. Note the downward shift in the second semi-annual period. For the 10-year Government Bond yield, the most likely range in four and a half years is from 1% to 2%. The probability of being in this range is 34.13%.
In a recent post on SeekingAlpha, we pointed out that a forecast of “heads” or “tails” in a coin flip leaves out critical information. What a sophisticated bettor needs to know is that, on average for a fair coin, the probability of heads is 50%. A forecast that the next coin flip will be “heads” is literally worth nothing to investors because the outcome is purely random.
The same is true for interest rates.
In this section we present the detailed probability distribution for both the 3-month bill rate and the 5-year Government Bond yield for 10 and 4.5 years forward using semi-annual time steps[1]. We present the probability of where rates will be at each time step in 1 percent “rate buckets.” The forecast for 3-month bill yields is shown in this graph:

3-Month Bill Yield Data:
The probability that the 3-month bill yield will be between 1% and 2% in 2 years is shown in column 4: 34.09%. The probability that the 3-month yield will be negative (as it has been often in Europe and Japan) in 2 years is 8.81% plus 0.55% plus 0.02% plus 0.00% = 9.37% (difference due to rounding). Cells shaded in blue represent positive probabilities of occurring, but the probability has been rounded to the nearest 0.01%. The shading scheme is defined as follows:
- Dark blue: the probability is greater than 0% but less than 1%
- Light blue: the probability is greater than or equal to 1% and less than 5%
- Light yellow: the probability is greater than or equal to 5% and 10%
- Medium yellow: the probability is greater than or equal to 10% and less than 20%
- Orange: the probability is greater than or equal to 20% and less than 25%
- Red: the probability is greater than 25%
The chart below shows the same probabilities for the 5-year Government Bond yield derived as part of the same simulation.

5-Year Swedish Government Bond Yield Data:
Modeling International Yield and Foreign Exchange Rate Correlation
The simulation of the Swedish Government Bond yield curve and the Krona exchange rate is done simultaneously with simulations of risk-free government yield curves in multiple countries. This simulation is based in daily historical data from 1962 (U.S.), 1974 (Japan), 1979 (United Kingdom), 1997 (Germany) and six other countries. The forward-looking correlation between Swedish Government Bond and U.S. Treasury 5-year zero coupon yields one year forward is given here:

Appendix: Government Bond Yield Simulation Methodology
The Government Bond yield probabilities are derived using the same methodology that SAS Institute Inc. recommends to its KRIS® and Kamakura Risk Manager® clients. A moderately technical explanation is given later in the appendix, but we summarize it briefly first.
Step 1: We take the closing Government Bond yield curve as our starting point.
Step 2: We use the number of points on the yield curve that best explains historical yield curve shifts. We note in the following graph that Government Bond yields span (by rate level and maturity) 31.36% of the historical experience in 14 countries:

For the highest degree of realism in a forward-looking simulation, using the international database is essential. Using daily government bond yield data from 14 countries from 1962 through December 31, 2024, we conclude that 12 “factors” drive almost all movements of government bond yields. The countries on which the analysis is based are Australia, Canada, France, Germany, Italy, Japan, New Zealand. Russia, Singapore, Spain, Sweden, Thailand, the United Kingdom, and the United States of America. No data from Russia is included after January 2022. The factors are related to 12 points on the yield curve. Because the Swedish Government Bond yield data reflect a maximum maturity of 10 years, only 8 of the 12 factors are used in this simulation. Those points and the order in which they are added to the model are shown here:

Step 3: We measure the volatility of changes in those factors and how volatility has changed over the same period.
Step 4: Using those measured volatilities, we generate 100,000 random shocks at each step and derive the resulting yield curve.
Step 5: We “validate” the model to make sure that the simulation EXACTLY prices the starting Government Bond curve and that it fits history as well as possible. The methodology for doing this is described below.
Step 6: We take all 100,000 simulated yield curves and calculate the probabilities that yields fall in each of the 1% “buckets” displayed in the graph.
Do Nominal Yields Accurately Reflect Expected Future Inflation?
We showed in a recent post on SeekingAlpha that, on average, investors have almost always done better by buying long term bonds than by rolling over short term Treasury bills in the United States. That means that market participants have generally (but not always) been accurate in forecasting future inflation and adding a risk premium to that forecast. This study is being updated using the 14-country data set in the coming weeks.
Technical Details
Daily government bond yields from the 14 countries listed above form the base historical data for fitting the number of yield curve factors and their volatility. The Government Bond historical data is provided by the Sveriges Riksbank. The use of the international bond data increases the number of observations to more than 109,000 and provides a more complete range of experience with both high rates and negative rates than a Swedish Government Bond data set alone provides.
The modeling process was published in a very important paper by David Heath, Robert Jarrow and Andrew Morton in 1992:

Professor Jarrow’s biography is available here.
The no-arbitrage foreign exchange rate simulation is based on this well-known paper by Amin and Jarrow:

For technically inclined readers, we recommend Prof. Jarrow’s book Modeling Fixed Income Securities and Interest Rate Options for those who want to know exactly how the “HJM” model construction works.

The number of factors, 12 for the 14-country model, has been stable since June 30, 2017.
Footnotes:
[1] The actual simulation uses 91-day time steps and spans a 10-year time horizon.


